6.8. Newton’s Method for Optimization#
Newton’s method can be used to find a local minimum or maximum of a function \(f(x)\). To find the extrema of a function, we replace \(f\) with \(f'\) and \(f'\) with \(f''\) in Newton’s root-finding method. The iteration formula is
(6.78)#\[\begin{equation}
x_{n+1} = x_{n} - \frac{f'(x_n)}{f''(x_n)}.
\end{equation}\]
Problem
Explain why we replace \(f\) with \(f'\) and \(f'\) with \(f''\) in Newton’s root-finding method when searching for extrema.
Solution
At a local minimum or maximum, the derivative \(f'(x) = 0\). Therefore, finding an extremum is equivalent to finding a root of \(f'(x)\).
Newton’s method for finding a root of a function \(g(x)\) uses the formula
(6.79)#\[\begin{equation}
x_{n+1} = x_n - \frac{g(x_n)}{g'(x_n)}.
\end{equation}\]
To find where \(f'(x) = 0\), we set \(g(x) = f'(x)\). Then \(g'(x) = f''(x)\), and Newton’s formula becomes
(6.80)#\[\begin{equation}
x_{n+1} = x_n - \frac{f'(x_n)}{f''(x_n)}.
\end{equation}\]
Thus, we are applying Newton’s root-finding method to the derivative \(f'(x)\), which requires us to use the second derivative \(f''(x)\).
The method can be extended to multiple dimensions
(6.81)#\[\begin{equation}
\mathbf{x}_{n+1} = \mathbf{x}_n - H_f(\mathbf{x}_n)^{-1} \nabla f(\mathbf{x}_n)
\end{equation}\]
where
\(\nabla f(\mathbf{x})\) is the gradient (first derivative)
\(H_f(\mathbf{x})\) is the Hessian matrix (second derivative for multidimensional problems)
The Hessian matrix is
(6.82)#\[\begin{equation}
H_f(\mathbf{x}) =
\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
\end{bmatrix}.
\end{equation}\]
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
from IPython.display import display, Image
from IPython.display import HTML
from jax import grad, hessian
import jax.numpy as jnp
from functools import partial
Here is Newton method for root finding code.
def newtons_method(f, x0, max_iter=1000, tol=1e-6, monitor=False):
"""
Newton's method for optimization using JAX automatic differentiation.
Parameters
----------
f : callable
Objective function to minimize
x0 : array_like
Initial guess
max_iter : int
Maximum number of iterations
tol : float
Convergence tolerance
monitor : bool
If True, return history of function values
Returns
-------
x_min : ndarray
Estimated minimum point
loss : list (optional)
History of function values if monitor=True
"""
x = jnp.array(x0, dtype=float)
# Gradient and Hessian functions via JAX
df = grad(f)
ddf = hessian(f)
if monitor:
loss = [f(x)]
# Newton's method loop
for i in range(max_iter):
# Evaluate gradient and Hessian
grad_val = df(x)
hess_val = ddf(x)
# Newton's update: solve H*delta = -grad for delta
delta_x = jnp.linalg.solve(hess_val, -grad_val)
x_new = x + delta_x
if monitor:
loss.append(f(x_new))
# Check convergence
if jnp.linalg.norm(delta_x) < tol:
print(f"Converged in {i+1} iterations")
if monitor:
return x_new, loss
else:
return x_new
x = x_new
print(f"Did not converge within {max_iter} iterations")
if monitor:
return x, loss
else:
return x
Example: Solving a Nonlinear System Using Least Squares
Consider finding the solution to the nonlinear system, a function I got from Wikipedia,
(6.83)#\[\begin{equation}
\begin{cases}
f_0 = 3x_0 - \cos(x_1 x_2) - \frac{3}{2} = 0 \\
f_1 = 4x_0^2 - 625x_1^2 + 2x_1 - 1 = 0 \\
f_2 = e^{-x_0 x_1} + 20x_2 + \frac{10\pi - 3}{3} = 0
\end{cases}
\end{equation}\]
We can solve this using Newton’s optimization method by minimizing the objective function
(6.84)#\[\begin{equation}
g(\mathbf{x}) = \frac{1}{2} \mathbf{F} \cdot \mathbf{F} = \frac{1}{2}\sum_{i=0}^{2} f_i^2,
\end{equation}\]
where \(\mathbf{F} = [f_0, f_1, f_2]^T\).
Minimizing \(g(\mathbf{x})\) is equivalent to minimizing the squared norm \(\|\mathbf{F}\|^2\).
def wiki_func(z):
x0, x1, x2 = z
f0=3*x0 - jnp.cos(x1*x2) - 3/2
f1=4*x0**2 - 625*x1**2 + 2*x1 - 1
f2=jnp.exp(-x0*x1) + 20*x2 + (10*jnp.pi-3)/3
return jnp.array([f0, f1, f2])
def objective(z):
f=wiki_func(z)
return jnp.dot(f,f)/2.0
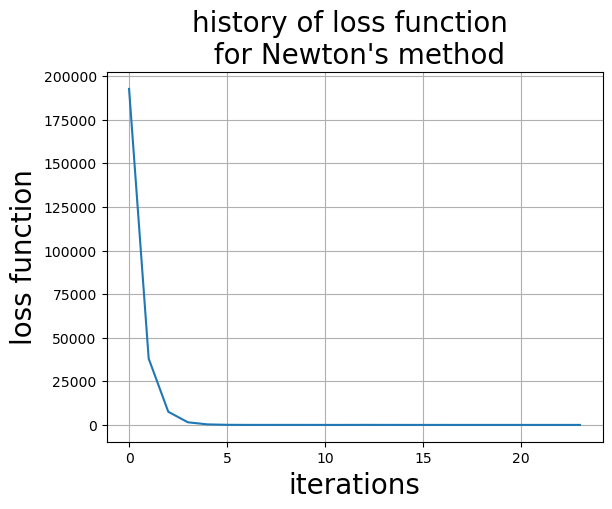
x, loss_newton=newtons_method(objective, jnp.ones(3), monitor=True)
print("Solution and objective", x, objective(x))
Converged in 23 iterations
Solution and objective [ 0.8331966 0.05494366 -0.5213615 ] 7.1054274e-15
# check solution
wiki_func(x)
Array([0.0000000e+00, 1.1920929e-07, 0.0000000e+00], dtype=float32)
ax=plt.subplot()
ax.set_title("history of loss function \n for Newton's method", size=20)
ax.set_xlabel("iterations", size=20)
ax.set_ylabel("loss function", size=20)
ax.plot(loss_newton)
ax.grid()
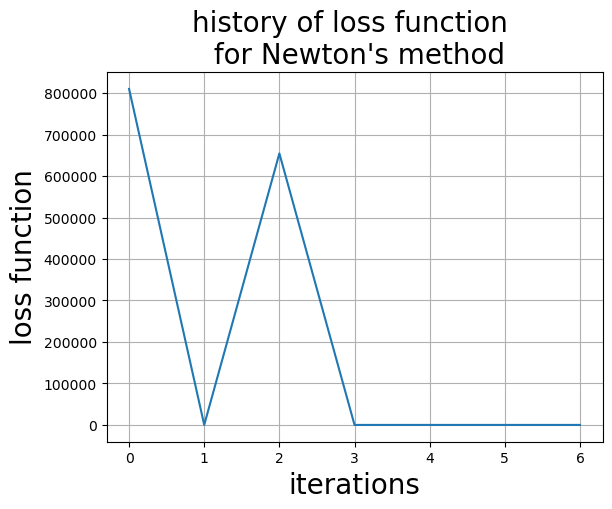
Example Minimize the Rosenbrock function
(6.85)#\[\begin{equation}
(1-x)^2 + 100(y-x^2)^2,
\end{equation} \]
which has a minima at \((x,y)=(1,1)\). How does Newton’s method do?
def rosenbrock(X):
# minima at 1,1
x, y = X
return (1 - x)**2 + 100 * (y - x**2)**2
x, loss_newton=newtons_method(rosenbrock, jnp.ones(2)*10, monitor=True)
print("Solution and objective", x, rosenbrock(x))
Converged in 6 iterations
Solution and objective [1. 1.] 0.0
ax=plt.subplot()
ax.set_title("history of loss function \n for Newton's method", size=20)
ax.set_xlabel("iterations", size=20)
ax.set_ylabel("loss function", size=20)
ax.plot(loss_newton)
ax.grid()
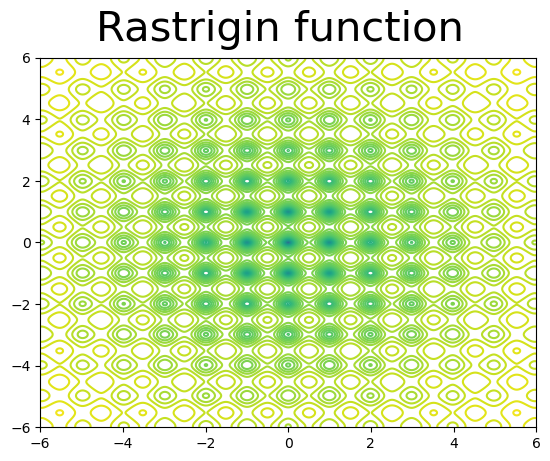
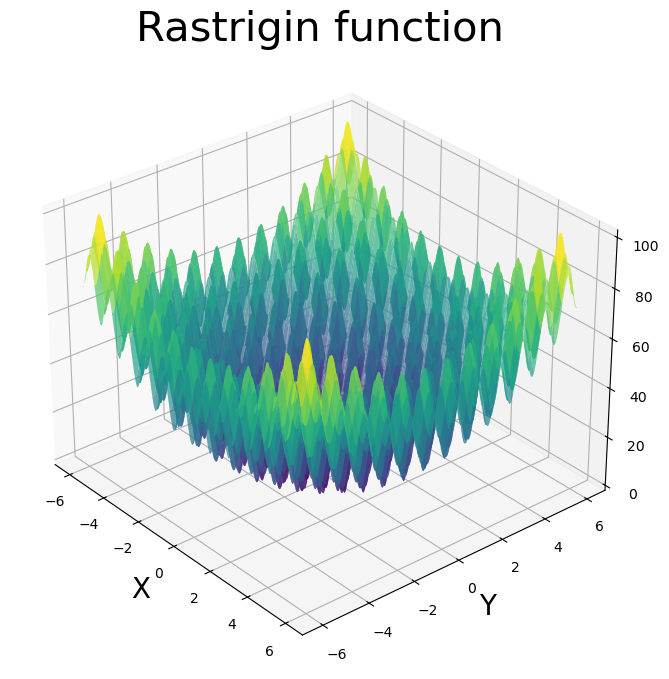
Example Try Newton’s method on the Rastrigin function. The Rastrigin function is non-convex and has many local minima, with a global minima at \((x,y)=(0,0)\).
(6.86)#\[\begin{equation}
f(x,y)= 20 + x^2 + y^2 - 10 (\cos(2 \pi x) +\cos(2 \pi y))
\end{equation} \]
def rastrigin(X):
#minima at 0, 0
# many local minima
x, y = X
return 20 + x**2 + y**2 - 10 * (jnp.cos(2 * jnp.pi * x) + jnp.cos(2 * jnp.pi * y))
x=np.linspace(-6,6,1000)
y=np.linspace(-6,6,1000)
fig=plt.figure()
fig.suptitle("Rastrigin function", size=30)
ax=fig.add_subplot()
X,Y=np.meshgrid(x,y)
Z=rastrigin([X,Y])
ax.contour(X,Y,np.log(Z), levels=50)
<matplotlib.contour.QuadContourSet at 0x7f83cc9ddd90>
X, Y = np.meshgrid(x, y)
Z = rastrigin([X,Y])
# Create the figure and axes object
fig = plt.figure(figsize=(8, 10))
ax = fig.add_subplot(111, projection='3d')
# Plot the surface
ax.plot_surface(X, Y, Z, cmap='viridis', alpha=.7)
# Set labels and title
ax.set_xlabel('X', size=20)
ax.set_ylabel('Y', size=20)
ax.set_title('Rastrigin function', size=30 )
ax.view_init(azim=-40)
x, loss_newton=newtons_method(rastrigin, jnp.ones(2)*5, tol=1e-10,monitor=True)
print("Solution and objective", x, rastrigin(x))
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
/tmp/ipykernel_3440/4255784910.py in <cell line: 0>()
----> 1 x, loss_newton=newtons_method(rastrigin, jnp.ones(2)*5, tol=1e-10,monitor=True)
2 print("Solution and objective", x, rastrigin(x))
/tmp/ipykernel_3440/4170161064.py in newtons_method(f, x0, max_iter, tol, monitor)
36 # Evaluate gradient and Hessian
37 grad_val = df(x)
---> 38 hess_val = ddf(x)
39
40 # Newton's update: solve H*delta = -grad for delta
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api.py in jacfun(*args, **kwargs)
694 if not has_aux:
695 pushfwd: Callable = partial(_jvp, f_partial, dyn_args)
--> 696 y, jac = vmap(pushfwd, out_axes=(None, -1))(_std_basis(dyn_args))
697 else:
698 pushfwd: Callable = partial(_jvp, f_partial, dyn_args, has_aux=True)
[... skipping hidden 1 frame]
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api.py in vmap_f(*args, **kwargs)
1156 out_axes_thunk=out_axes_thunk)
1157 else:
-> 1158 out_flat = batching.batch(
1159 flat_fun, axis_data, in_axes_flat,
1160 lambda: flatten_axes("vmap out_axes", out_tree(), out_axes)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in call_wrapped(self, *args, **kwargs)
210 def call_wrapped(self, *args, **kwargs):
211 """Calls the transformed function"""
--> 212 return self.f_transformed(*args, **kwargs)
213
214 def __repr__(self):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/batching.py in _batch_outer(f, axis_data, in_dims, *in_vals)
701 tag = TraceTag()
702 with source_info_util.transform_name_stack('vmap'):
--> 703 outs, trace = f(tag, in_dims, *in_vals)
704 with core.ensure_no_leaks(trace): del trace
705 return outs
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/batching.py in _batch_inner(f, axis_data, out_dim_dests, tag, in_dims, *in_vals)
717 core.extend_axis_env_nd([(axis_data.name, axis_data.size)]),
718 core.add_spmd_axis_names(axis_data.spmd_name)):
--> 719 outs = f(*in_tracers)
720 out_dim_dests = out_dim_dests() if callable(out_dim_dests) else out_dim_dests
721 out_vals = map(partial(from_elt, trace, axis_data.size, axis_data.explicit_mesh_axis),
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/batching.py in flatten_fun_for_vmap(f, store, in_tree, *args_flat)
398 store: lu.Store, in_tree: PyTreeDef, *args_flat):
399 py_args, py_kwargs = tree_unflatten(in_tree, args_flat)
--> 400 ans = f(*py_args, **py_kwargs)
401 ans, out_tree = tree_flatten(ans, is_leaf=is_vmappable)
402 store.store(out_tree)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in _get_result_paths_thunk(_fun, _store, *args, **kwargs)
419 @transformation_with_aux2
420 def _get_result_paths_thunk(_fun: Callable, _store: Store, *args, **kwargs):
--> 421 ans = _fun(*args, **kwargs)
422 result_paths = tuple(f"result{_clean_keystr_arg_names(path)}" for path, _ in generate_key_paths(ans))
423 if _store:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api.py in _jvp(fun, primals, tangents, has_aux)
1913 if not has_aux:
1914 flat_fun, out_tree = flatten_fun_nokwargs(fun, tree_def)
-> 1915 out_primals, out_tangents = ad.jvp(flat_fun).call_wrapped(ps_flat, ts_flat)
1916 out_tree = out_tree()
1917 return (tree_unflatten(out_tree, out_primals),
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in call_wrapped(self, *args, **kwargs)
210 def call_wrapped(self, *args, **kwargs):
211 """Calls the transformed function"""
--> 212 return self.f_transformed(*args, **kwargs)
213
214 def __repr__(self):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in jvpfun(f, instantiate, transform_stack, primals, tangents)
83 else contextlib.nullcontext())
84 with ctx:
---> 85 out_primals, out_tangents = f(tag, primals, tangents)
86 if type(instantiate) is bool:
87 instantiate = [instantiate] * len(out_tangents)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in jvp_subtrace(f, tag, primals, tangents)
136 for x, t in zip(primals, tangents)]
137 with core.set_current_trace(trace):
--> 138 ans = f(*in_tracers)
139 out = unzip2(map(trace.to_primal_tangent_pair, ans))
140 return out
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api_util.py in flatten_fun_nokwargs(f, store, in_tree, *args_flat)
88 in_tree: PyTreeDef, *args_flat):
89 py_args = tree_unflatten(in_tree, args_flat)
---> 90 ans = f(*py_args)
91 ans, out_tree = tree_flatten(ans)
92 store.store(out_tree)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api_util.py in _argnums_partial(_fun, _dyn_argnums, _fixed_args, *dyn_args, **kwargs)
290 args = [next(fixed_args_).val if x is sentinel else x for x in args]
291 assert next(fixed_args_, sentinel) is sentinel
--> 292 return _fun(*args, **kwargs)
293
294 def argnames_partial_except(f: lu.WrappedFun, static_argnames: tuple[str, ...],
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in _get_result_paths_thunk(_fun, _store, *args, **kwargs)
419 @transformation_with_aux2
420 def _get_result_paths_thunk(_fun: Callable, _store: Store, *args, **kwargs):
--> 421 ans = _fun(*args, **kwargs)
422 result_paths = tuple(f"result{_clean_keystr_arg_names(path)}" for path, _ in generate_key_paths(ans))
423 if _store:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api.py in jacfun(*args, **kwargs)
786 tree_map(partial(_check_input_dtype_jacrev, holomorphic, allow_int), dyn_args)
787 if not has_aux:
--> 788 y, pullback = _vjp(f_partial, *dyn_args)
789 else:
790 y, pullback, aux = _vjp(f_partial, *dyn_args, has_aux=True)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api.py in _vjp(fun, has_aux, *primals)
2188 if not has_aux:
2189 flat_fun, out_tree = flatten_fun_nokwargs(fun, in_tree)
-> 2190 out_primals, vjp = ad.vjp(flat_fun, primals_flat)
2191 out_tree = out_tree()
2192 else:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in vjp(traceable, primals, has_aux)
311 def vjp(traceable: lu.WrappedFun, primals, has_aux=False):
312 if not has_aux:
--> 313 out_primals, pvals, jaxpr, consts = linearize(traceable, *primals)
314 else:
315 out_primals, pvals, jaxpr, consts, aux = linearize(traceable, *primals, has_aux=True)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in linearize(traceable, *primals, **kwargs)
285 has_aux = kwargs.pop('has_aux', False)
286 if config.use_direct_linearize.value:
--> 287 return direct_linearize(traceable, primals, kwargs, has_aux=has_aux)
288 if not has_aux:
289 jvpfun = jvp(traceable)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in direct_linearize(traceable, primals, kwargs, has_aux, tag)
259 else x for x in aux]
260 else:
--> 261 ans = traceable.call_wrapped(*tracers)
262 aux = None
263 out_primals, out_tangents = unzip2(map(linearize_trace.to_primal_tangent_pair, ans))
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in call_wrapped(self, *args, **kwargs)
210 def call_wrapped(self, *args, **kwargs):
211 """Calls the transformed function"""
--> 212 return self.f_transformed(*args, **kwargs)
213
214 def __repr__(self):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api_util.py in flatten_fun_nokwargs(f, store, in_tree, *args_flat)
88 in_tree: PyTreeDef, *args_flat):
89 py_args = tree_unflatten(in_tree, args_flat)
---> 90 ans = f(*py_args)
91 ans, out_tree = tree_flatten(ans)
92 store.store(out_tree)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/api_util.py in _argnums_partial(_fun, _dyn_argnums, _fixed_args, *dyn_args, **kwargs)
290 args = [next(fixed_args_).val if x is sentinel else x for x in args]
291 assert next(fixed_args_, sentinel) is sentinel
--> 292 return _fun(*args, **kwargs)
293
294 def argnames_partial_except(f: lu.WrappedFun, static_argnames: tuple[str, ...],
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in _get_result_paths_thunk(_fun, _store, *args, **kwargs)
419 @transformation_with_aux2
420 def _get_result_paths_thunk(_fun: Callable, _store: Store, *args, **kwargs):
--> 421 ans = _fun(*args, **kwargs)
422 result_paths = tuple(f"result{_clean_keystr_arg_names(path)}" for path, _ in generate_key_paths(ans))
423 if _store:
/tmp/ipykernel_3440/3128212555.py in rastrigin(X)
3 # many local minima
4 x, y = X
----> 5 return 20 + x**2 + y**2 - 10 * (jnp.cos(2 * jnp.pi * x) + jnp.cos(2 * jnp.pi * y))
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/numpy/array_methods.py in op(self, *args)
1139 def _forward_operator_to_aval(name):
1140 def op(self, *args):
-> 1141 return getattr(self.aval, f"_{name}")(self, *args)
1142 return op
1143
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/numpy/array_methods.py in deferring_binary_op(self, other)
602 args = (other, self) if swap else (self, other)
603 if isinstance(other, _accepted_binop_types):
--> 604 return binary_op(*args)
605 # Note: don't use isinstance here, because we don't want to raise for
606 # subclasses, e.g. NamedTuple objects that may override operators.
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/numpy/ufuncs.py in power(x1, x2)
2681 else:
2682 x1, = promote_dtypes_numeric(x1)
-> 2683 return lax.integer_pow(x1, x2)
2684
2685 # Handle cases #2 and #3 under a jit:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/lax/lax.py in integer_pow(x, y)
944 .. _stablehlo.multiply: https://openxla.org/stablehlo/spec#multiply
945 """
--> 946 return integer_pow_p.bind(x, y=y)
947
948
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind(self, *args, **params)
630 def bind(self, *args, **params):
631 args = args if self.skip_canonicalization else map(canonicalize_value, args)
--> 632 return self._true_bind(*args, **params)
633
634 def _true_bind(self, *args, **params):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in _true_bind(self, *args, **params)
646 trace_ctx.set_trace(eval_trace)
647 try:
--> 648 return self.bind_with_trace(prev_trace, args, params)
649 finally:
650 trace_ctx.set_trace(prev_trace)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind_with_trace(self, trace, args, params)
658 with set_current_trace(trace):
659 return self.to_lojax(*args, **params) # type: ignore
--> 660 return trace.process_primitive(self, args, params)
661 trace.process_primitive(self, args, params) # may raise lojax error
662 raise Exception(f"couldn't apply typeof to args: {args}")
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in process_primitive(self, primitive, args, params)
922 lin = primitive_linearizations.get(primitive, fallback)
923 with core.set_current_trace(self.parent_trace):
--> 924 primal_out, tangent_nzs_out, residuals, linearized = lin(
925 tangent_nzs, *primals_in, **params)
926 with (core.set_current_trace(self.tangent_trace),
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in fallback_linearize_rule(_prim, _nonzeros, *primals, **params)
1133 raise NotImplementedError(msg)
1134 debug_jvp = debug_info("linearize_prim_jvp", jvp, primals, params)
-> 1135 return linearize_from_jvp(lu.wrap_init(jvp, debug_info=debug_jvp),
1136 _prim.multiple_results, _nonzeros, False, False,
1137 primals, params)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in linearize_from_jvp(jvp, multiple_results, nonzeros, user_facing_symbolic_zeros, instantiate_input_zeros, primals, params)
1167 tangent_args = [trace.new_arg(pe.PartialVal.unknown(a)) if nz else make_zero(a)
1168 for a, nz in zip(tangent_avals, nonzeros)]
-> 1169 out_primals, out_tangents = jvp.call_wrapped(
1170 tuple(primals), tuple(tangent_args), **params)
1171
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in call_wrapped(self, *args, **kwargs)
210 def call_wrapped(self, *args, **kwargs):
211 """Calls the transformed function"""
--> 212 return self.f_transformed(*args, **kwargs)
213
214 def __repr__(self):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/linear_util.py in _get_result_paths_thunk(_fun, _store, *args, **kwargs)
419 @transformation_with_aux2
420 def _get_result_paths_thunk(_fun: Callable, _store: Store, *args, **kwargs):
--> 421 ans = _fun(*args, **kwargs)
422 result_paths = tuple(f"result{_clean_keystr_arg_names(path)}" for path, _ in generate_key_paths(ans))
423 if _store:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in standard_jvp(jvprules, primitive, primals, tangents, **params)
1291
1292 def standard_jvp(jvprules, primitive, primals, tangents, **params):
-> 1293 val_out = primitive.bind(*primals, **params)
1294 tangents_out = [rule(t, *primals, **params) for rule, t in zip(jvprules, tangents)
1295 if rule is not None and type(t) is not Zero]
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind(self, *args, **params)
630 def bind(self, *args, **params):
631 args = args if self.skip_canonicalization else map(canonicalize_value, args)
--> 632 return self._true_bind(*args, **params)
633
634 def _true_bind(self, *args, **params):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in _true_bind(self, *args, **params)
646 trace_ctx.set_trace(eval_trace)
647 try:
--> 648 return self.bind_with_trace(prev_trace, args, params)
649 finally:
650 trace_ctx.set_trace(prev_trace)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind_with_trace(self, trace, args, params)
658 with set_current_trace(trace):
659 return self.to_lojax(*args, **params) # type: ignore
--> 660 return trace.process_primitive(self, args, params)
661 trace.process_primitive(self, args, params) # may raise lojax error
662 raise Exception(f"couldn't apply typeof to args: {args}")
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/partial_eval.py in process_primitive(self, primitive, tracers, params)
222 return custom_partial_eval_rules[primitive](self, *tracers, **params)
223 else:
--> 224 return self.default_process_primitive(primitive, tracers, params)
225
226 def default_process_primitive(self, primitive, tracers, params):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/partial_eval.py in default_process_primitive(self, primitive, tracers, params)
231 consts = [t.pval.get_known() for t in tracers]
232 if all(c is not None for c in consts):
--> 233 return primitive.bind_with_trace(self.parent_trace, consts, params)
234 tracers = map(self.instantiate_const, tracers)
235 avals = [t.aval for t in tracers]
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind_with_trace(self, trace, args, params)
658 with set_current_trace(trace):
659 return self.to_lojax(*args, **params) # type: ignore
--> 660 return trace.process_primitive(self, args, params)
661 trace.process_primitive(self, args, params) # may raise lojax error
662 raise Exception(f"couldn't apply typeof to args: {args}")
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in process_primitive(self, primitive, tracers, params)
687 raise NotImplementedError(msg)
688 with core.set_current_trace(self.parent_trace):
--> 689 primal_out, tangent_out = jvp(primals_in, tangents_in, **params)
690
691 if primitive.multiple_results:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in standard_jvp(jvprules, primitive, primals, tangents, **params)
1292 def standard_jvp(jvprules, primitive, primals, tangents, **params):
1293 val_out = primitive.bind(*primals, **params)
-> 1294 tangents_out = [rule(t, *primals, **params) for rule, t in zip(jvprules, tangents)
1295 if rule is not None and type(t) is not Zero]
1296 return val_out, functools.reduce(add_tangents, tangents_out, Zero.from_primal_value(val_out))
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/ad.py in <listcomp>(.0)
1292 def standard_jvp(jvprules, primitive, primals, tangents, **params):
1293 val_out = primitive.bind(*primals, **params)
-> 1294 tangents_out = [rule(t, *primals, **params) for rule, t in zip(jvprules, tangents)
1295 if rule is not None and type(t) is not Zero]
1296 return val_out, functools.reduce(add_tangents, tangents_out, Zero.from_primal_value(val_out))
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/lax/lax.py in _integer_pow_jvp(g, x, y)
4566
4567 def _integer_pow_jvp(g, x, *, y):
-> 4568 return _zeros(g) if y == 0 else mul(g, mul(_const(x, y), integer_pow(x, y - 1)))
4569
4570 integer_pow_p = standard_primitive(
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/lax/lax.py in mul(x, y)
1245 """
1246 x, y = core.standard_insert_pvary(x, y)
-> 1247 return mul_p.bind(x, y)
1248
1249 @export
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind(self, *args, **params)
630 def bind(self, *args, **params):
631 args = args if self.skip_canonicalization else map(canonicalize_value, args)
--> 632 return self._true_bind(*args, **params)
633
634 def _true_bind(self, *args, **params):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in _true_bind(self, *args, **params)
646 trace_ctx.set_trace(eval_trace)
647 try:
--> 648 return self.bind_with_trace(prev_trace, args, params)
649 finally:
650 trace_ctx.set_trace(prev_trace)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind_with_trace(self, trace, args, params)
658 with set_current_trace(trace):
659 return self.to_lojax(*args, **params) # type: ignore
--> 660 return trace.process_primitive(self, args, params)
661 trace.process_primitive(self, args, params) # may raise lojax error
662 raise Exception(f"couldn't apply typeof to args: {args}")
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/batching.py in process_primitive(self, p, tracers, params)
588 elif p in primitive_batchers:
589 with core.set_current_trace(self.parent_trace):
--> 590 val_out, dim_out = primitive_batchers[p](vals_in, dims_in, **params)
591 else:
592 raise NotImplementedError(f"Batching rule for '{p}' not implemented")
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/interpreters/batching.py in broadcast_batcher(prim, args, dims, **params)
1095 for x, d in zip(args, dims) if np.ndim(x)):
1096 # if there's only agreeing batch dims and scalars, just call the primitive
-> 1097 out = prim.bind(*args, **params)
1098 return (out, (dim,) * len(out)) if prim.multiple_results else (out, dim)
1099 else:
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind(self, *args, **params)
630 def bind(self, *args, **params):
631 args = args if self.skip_canonicalization else map(canonicalize_value, args)
--> 632 return self._true_bind(*args, **params)
633
634 def _true_bind(self, *args, **params):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in _true_bind(self, *args, **params)
646 trace_ctx.set_trace(eval_trace)
647 try:
--> 648 return self.bind_with_trace(prev_trace, args, params)
649 finally:
650 trace_ctx.set_trace(prev_trace)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in bind_with_trace(self, trace, args, params)
658 with set_current_trace(trace):
659 return self.to_lojax(*args, **params) # type: ignore
--> 660 return trace.process_primitive(self, args, params)
661 trace.process_primitive(self, args, params) # may raise lojax error
662 raise Exception(f"couldn't apply typeof to args: {args}")
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/core.py in process_primitive(self, primitive, args, params)
1187 args = map(full_lower, args)
1188 check_eval_args(args)
-> 1189 return primitive.impl(*args, **params)
1190
1191 def process_call(self, primitive, f, tracers, params):
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/dispatch.py in apply_primitive(prim, *args, **params)
92 prev = config.disable_jit.swap_local(False)
93 try:
---> 94 outs = fun(*args)
95 finally:
96 config.disable_jit.set_local(prev)
/opt/hostedtoolcache/Python/3.11.13/x64/lib/python3.11/site-packages/jax/_src/traceback_util.py in reraise_with_filtered_traceback(*args, **kwargs)
174 '''
175
--> 176 @functools.wraps(fun)
177 def reraise_with_filtered_traceback(*args, **kwargs):
178 __tracebackhide__ = True
KeyboardInterrupt:
ax=plt.subplot()
ax.set_title("history of loss function \n for Newton's method", size=20)
ax.set_xlabel("iterations", size=20)
ax.set_ylabel("loss function", size=20)
ax.plot(loss_newton, "-o")
ax.grid()
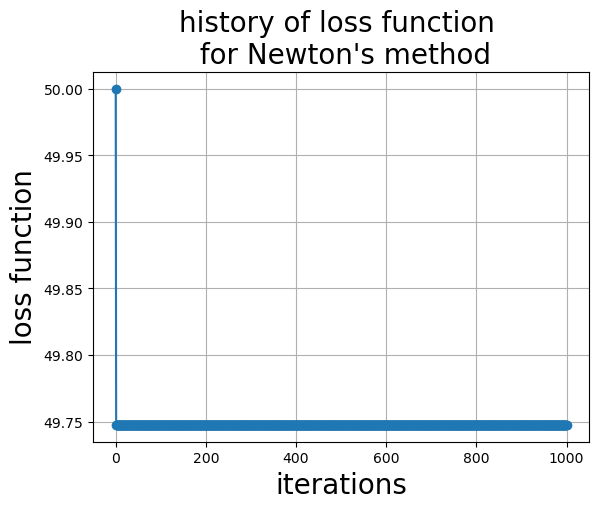
Question How did Newton’s method perform on the Rastrigin function? Did it find the global minima? Explain what happened. Can you think of anything you could do to help improve the result?